Algorytm Euklidesa to efektywna metoda wyznaczania Największego Wspólnego Dzielnika (NWD) dwóch liczb. Może służyć także do sprawdzania, czy dane liczby są względnie pierwsze, tzn. czy NWD(a, b)=1. Opiera się na zasadzie, że NWD dwóch liczb nie zmienia się, jeśli większą liczbę zastąpimy różnicą między większą a mniejszą liczbą. Proces ten jest powtarzany, aż jedna z liczb będzie równa zero, a wówczas druga liczba będzie szukanym NWD.
Istnieją dwie główne wersje Algorytmu Euklidesa: z resztą z dzielenia i z odejmowaniem. Kiedy mówi się o Algorytmie Euklidesa, zazwyczaj ma się na myśli tę pierwszą, efektywniejszą wersję, ponieważ reszta z dzielenia „skacze” o większe wartości niż odejmowanie. Nie wymaga on także rozkładania liczb na czynniki pierwsze.
🧮 Algorytm Euklidesa z resztą z dzielenia
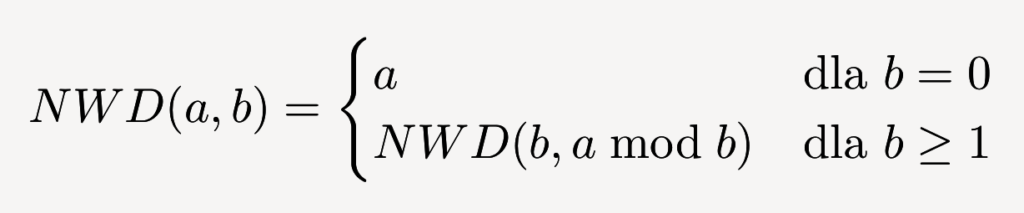
gdzie a mob b oznacza resztę z dzielenia liczby a przez liczbę b, na przykład 7 mod 5=2, 2 mod 5=2.
Jak to działa krok po kroku
Na początku mamy nasze dwie liczby, a i b. Przyjmujemy, że a jest większe lub równe b. Jeśli tak nie jest, po prostu zamienimy je miejscami. Następnie rozpoczynamy pętlę, która będzie trwać tak długo, dopóki nasza liczba b nie stanie się zerem. To sygnał, że dotarliśmy do celu.
W każdym obiegu tej pętli dzieją się trzy kluczowe rzeczy:
- Obliczamy resztę z dzielenia a przez b. Wynik tej operacji, czyli resztę (r), traktujemy jako nową, mniejszą liczbę. To właśnie ta reszta jest sercem efektywności algorytmu – ona reprezentuje tę część, która pozostała po odjęciu od a tylu razy b, ile się dało.
- Liczba b staje się nową liczbą a. W następnym kroku to poprzednia wartość b (czyli mniejsza z pary, którą mieliśmy) przejmuje rolę większej liczby a.
- Reszta (r) staje się nową liczbą b. A to, co było resztą z poprzedniego dzielenia, teraz staje się drugą liczbą, b, z którą będziemy dalej pracować.
Ten proces powtarza się w kółko: bierzemy dwie liczby, dzielimy większą przez mniejszą, a reszta staje się nową mniejszą liczbą, podczas gdy poprzednia mniejsza liczba staje się nową większą. Dzięki temu liczby w każdej iteracji maleją, aż w końcu b osiągnie zero. W tym momencie liczba a (ta, która przeżyła całe to dzielenie) jest naszym Największym Wspólnym Dzielnikiem.
Przykład zastosowania algorytmu z resztą z dzielenia
Obliczyć NWD (1348, 120).
| NWD (1348, 120)= | |
| = NWD (120, 1348 mod 120)= = NWD (120, 28)= | obliczamy resztę z dzielenia 1348 przez 120 czyli 1348 mod 120 = 28 |
| = NWD (28, 120 mod 28)= = NWD (28, 8)= | obliczamy resztę z dzielenia 120 przez 28 czyli 120 mod 28 = 8 |
| = NWD (8, 28 mod 8)= = NWD (8, 4)= | obliczamy resztę z dzielenia 28 przez 8 czyli 28 mod 8 = 4 |
| = NWD (4, 8 mod 4)= = NWD (4, 0)= | i wreszcie reszta z dzielenia 8 przez 4 jest równa 0, czyli 8 mod 4 = 0 |
| =4 | otrzymujemy NWD (1348, 120) = 4 |
🧮 Algorytm Euklidesa z odejmowaniem
Algorytm z odejmowaniem jest mniej efektywną i jednocześnie bardziej intuicyjną jego wersją. Nie wymaga skomplikowanych obliczeń, a jedynie powtarzalnego odejmowania tak długo, aż liczby a i b będą sobie równe. To sygnał, że znaleźliśmy NWD.
Przykład zastosowania algorytmu z odejmowaniem
Obliczyć NWD (1348, 120).
| NWD (1348, 120)= | |
| = NWD (120, 1348–120) = = NWD (120, 1228) = = NWD (120, 1228–120) = = NWD (120, 1108) = = NWD (120, 1108–120) = = NWD (120, 988) = = NWD (120, 988–120) = = NWD (120,868) = = NWD (120, 868–120) = = NWD (120, 748) = = NWD (120, 748–120) = = NWD (120, 628) = = NWD (120, 628–120) = = NWD (120, 508) = = NWD (120, 508–120) = = NWD (120, 388) = = NWD (120, 388–120) = = NWD (120, 268) = = NWD (120, 268–120) = = NWD (120, 148) = = NWD (120, 148–120) = = NWD (120, 28) = | Tak długo odejmujemy 120, aż otrzymamy liczbę co najwyżej równą 120. otrzymaliśmy 28, to jeszcze nie koniec. |
| = NWD (28, 120-28) = = NWD (28, 92) = = NWD (28, 92-28) = = NWD (28, 64) = = NWD (28, 64-28) = = NWD (28, 36) = = NWD (28, 36-28) = = NWD (28, 8) = | Liczby 120 i 28 jakby zamieniają się miejscami i teraz odejmujemy 28, tak długo, aż wynik będzie liczbą co najwyżej równą 28. |
| = NWD (8, 28-8) = = NWD (8, 20) = = NWD (8, 20-8) = = NWD (8, 12) = = NWD (8, 12-8) = = NWD (8, 4) = | Ponieważ otrzymaliśmy 8, zamieniamy liczby miejscami i teraz odejmujemy 8. Aby zakończyć, nasz wynik powinien być równy 8. Niestety, wyszło 4, więc to nie koniec. |
| = NWD (4, 8-4) = = NWD (4, 4) = | Liczba 4 staje się teraz liczbą a. W kolejnej iteracji odejmujemy 4 od 8. Otrzymaliśmy 4, (czyli a=b). Koniec. |
| =4 | otrzymujemy NWD (1348, 120) = 4 |
Zdecydowanie polecam Algorytm Euklidesa z resztą z dzielenia. Ten z odejmowaniem jest długi i żmudny.
Ważna uwaga:
Jestem autorem i właścicielem wszystkich tekstów, zdjęć, rysunków, infografik i wykresów na tym blogu, za wyjątkiem kilku, przy których podałam źródło, albo tych, które są rozpowszechniane na licencji Creative Commons. Jeśli chciałabyś lub chciałbyś skopiować treści tu umieszczone i wykorzystać je, w literaturze swojej pracy umieść źródło w postaci linka do strony, z której zostały przez Ciebie pobrane. Korzystaj z umieszczonych tu informacji i obrazów, ale nie podpisuj się pod nimi swoim nazwiskiem.